Our papers are the official record of our discoveries. They allow others to build on and apply our work. Each one is the result of many months of research, so we make a special effort to make our papers clear, inspiring and beautiful, and publish them in leading journals.
- Date
- Subject
- Theme
- Journal
- Citations
- Altmetric
- SNIP
- Author
 T. Fink
T. Fink Y. He
Y. He O. Gamayun
O. Gamayun J. Wang
J. Wang A. Stepanenko
A. Stepanenko M. Burtsev
M. Burtsev A. V. Kosyak
A. V. Kosyak E. Sobko
E. Sobko F. Sheldon
F. Sheldon F. Caravelli
F. Caravelli I. Shkredov
I. Shkredov A. Sarikyan
A. Sarikyan A. Esterov
A. Esterov A. Ochirov
A. Ochirov M. Reeves
M. Reeves G. Caldarelli
G. Caldarelli R. Hannam
R. Hannam A. Coolen
A. Coolen O. Dahlsten
O. Dahlsten A. Mozeika
A. Mozeika M. Bardoscia
M. Bardoscia P. Barucca
P. Barucca M. Rowley
M. Rowley I. Teimouri
I. Teimouri F. Antenucci
F. Antenucci A. Scala
A. Scala R. Farr
R. Farr A. Zegarac
A. Zegarac S. Sebastio
S. Sebastio B. Bollobás
B. Bollobás F. Lafond
F. Lafond D. Farmer
D. Farmer C. Pickard
C. Pickard T. Reeves
T. Reeves J. Blundell
J. Blundell A. Gallagher
A. Gallagher M. Przykucki
M. Przykucki P. Smith
P. Smith L. Pietronero
L. Pietronero
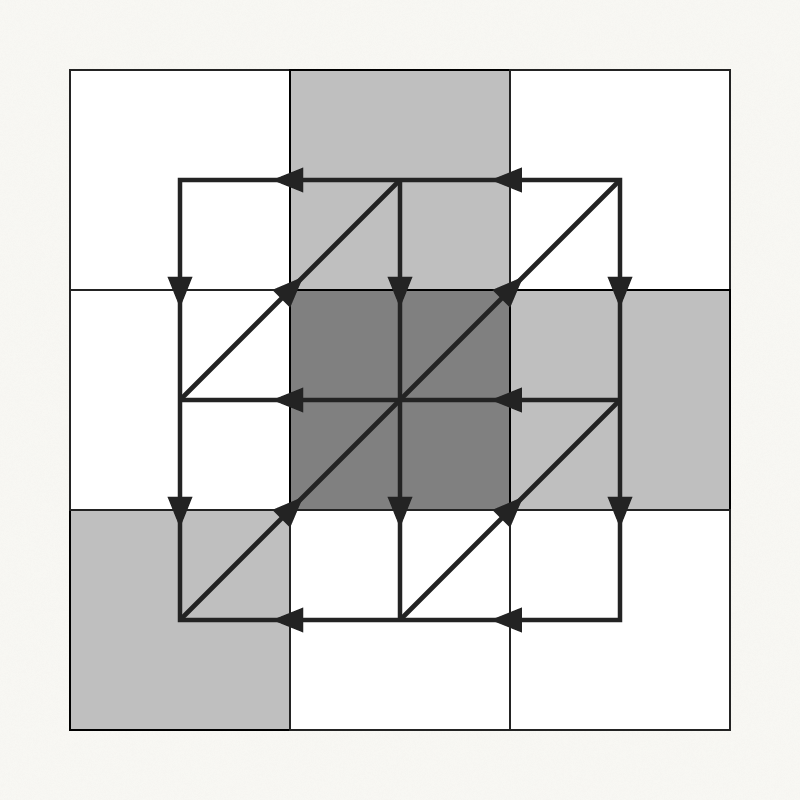
Percolation theory
Bootstrap percolation models
A subset of bootstrap percolation models, which stabilise systems of cells on infinite lattices, exhibit non-trivial phase transitions.
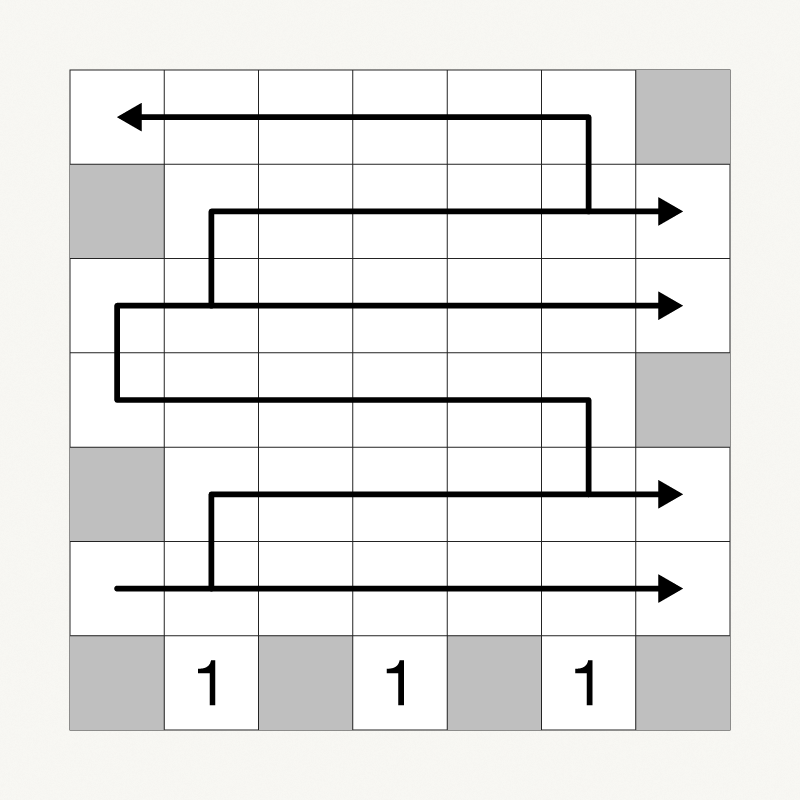
Percolation theory
Maximum percolation time
A simple formula gives the maximum time for an n x n grid to become entirely infected having undergone a bootstrap percolation process.

Percolation theory
Percolation on Galton-Watson trees
The critical probability for bootstrap percolation, a process which mimics the spread of an infection in a graph, is bounded for Galton-Watson trees.