Our papers are the official record of our discoveries. They allow others to build on and apply our work. Each one is the result of many months of research, so we make a special effort to make our papers clear, inspiring and beautiful, and publish them in leading journals.
- Date
- Subject
- Theme
- Journal
- Citations
- Altmetric
- SNIP
- Author
 M. Burtsev
M. Burtsev A. V. Kosyak
A. V. Kosyak J. Wang
J. Wang Y. He
Y. He O. Gamayun
O. Gamayun E. Sobko
E. Sobko F. Sheldon
F. Sheldon F. Caravelli
F. Caravelli I. Shkredov
I. Shkredov A. Stepanenko
A. Stepanenko A. Sarikyan
A. Sarikyan A. Esterov
A. Esterov A. Ochirov
A. Ochirov M. Reeves
M. Reeves T. Fink
T. Fink G. Caldarelli
G. Caldarelli R. Hannam
R. Hannam A. Coolen
A. Coolen O. Dahlsten
O. Dahlsten A. Mozeika
A. Mozeika M. Bardoscia
M. Bardoscia P. Barucca
P. Barucca M. Rowley
M. Rowley I. Teimouri
I. Teimouri F. Antenucci
F. Antenucci A. Scala
A. Scala R. Farr
R. Farr A. Zegarac
A. Zegarac S. Sebastio
S. Sebastio B. Bollobás
B. Bollobás F. Lafond
F. Lafond D. Farmer
D. Farmer C. Pickard
C. Pickard T. Reeves
T. Reeves J. Blundell
J. Blundell A. Gallagher
A. Gallagher M. Przykucki
M. Przykucki P. Smith
P. Smith L. Pietronero
L. Pietronero

Neurocomputing
Circuits with memory
We derive dynamical equations for networks with memristors and the Lyapunov functions of purely memristive circuits to study their stability.

Neurocomputing
Optimal electronic reservoirs
Balancing memory from linear components with nonlinearities from memristors optimises the computational capacity of electronic reservoirs.

Neurocomputing
Breaking classical barriers
Circuits of memristors, resistors with memory, can exhibit instabilities which allow classical tunnelling through potential energy barriers.
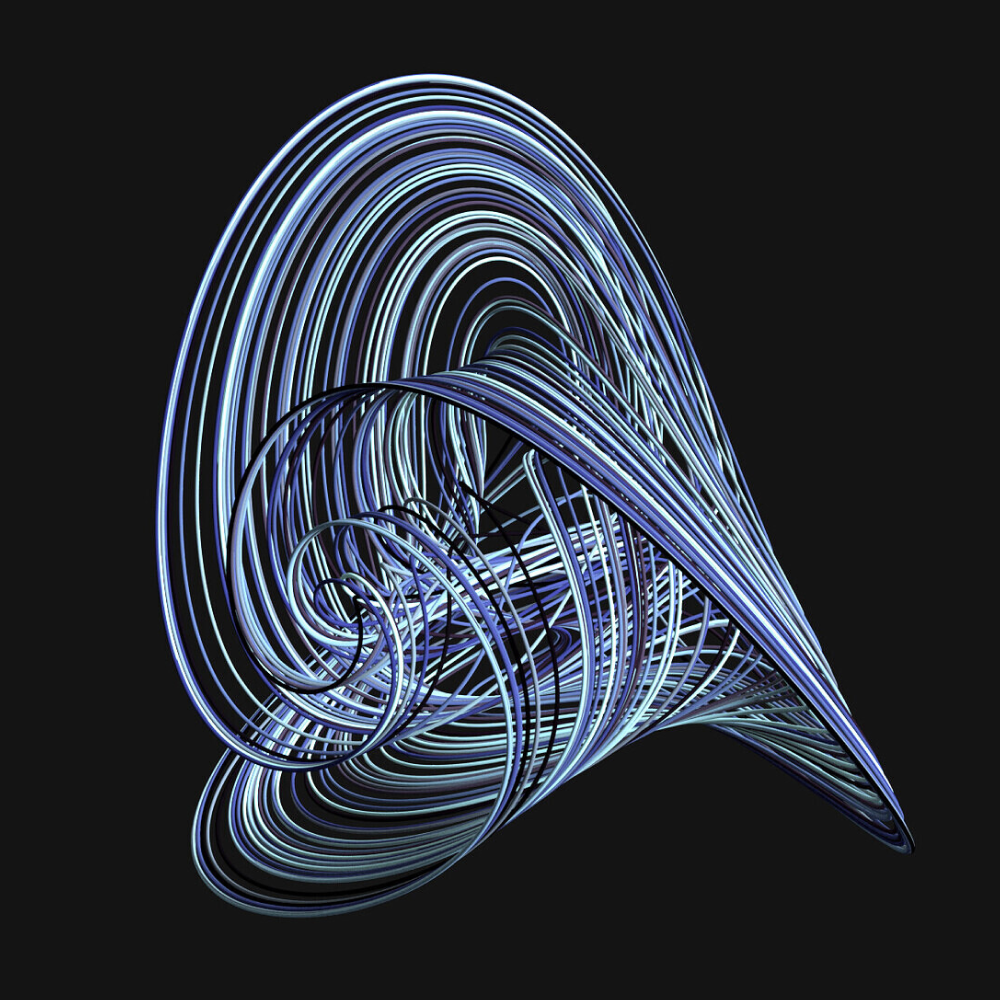
Neurocomputing
Memristive networks
A simple solvable model of memristive networks suggests a correspondence between the asymptotic states of memristors and the Ising model.
Neurocomputing
Solvable memristive circuits
Exact solutions for the dynamics of interacting memristors predict whether they relax to higher or lower resistance states given random initialisations.
Neurocomputing
Memristive networks and learning
Memristive networks preserve memory and have the ability to learn according to analysis of the network’s internal memory dynamics.
Neurocomputing
Dynamics of memristors
Exact equations of motion provide an analytical description of the evolution and relaxation properties of complex memristive circuits.
Complex networks
Optimal growth rates
An extension of the Kelly criterion maximises the growth rate of multiplicative stochastic processes when limited resources are available.
Financial markets
Instability in complex ecosystems
The community matrix of a complex ecosystem captures the population dynamics of interacting species and transitions to unstable abundances.
Percolation theory
Clusters of neurons
Percolation theory shows that the formation of giant clusters of neurons relies on a few parameters that could be measured experimentally.
Gravity
Cyclic isotropic cosmologies
In an infinitely bouncing Universe, the scalar field driving the cosmological expansion and contraction carries information between phases.
Neurocomputing
From memory to scale-free
A local model of preferential attachment with short-term memory generates scale-free networks, which can be readily computed by memristors.